Role of non-gaussian quantum fluctuations in neutrino entanglement
Prepared by Amol Patwardhan, with input from Denis Lacroix
In extreme astrophysical settings like core-collapse supernovae, neutrinos are the main carriers of energy and lepton number and are vital in driving the explosion mechanism and setting the conditions for element synthesis. Because of the flavor-dependence of neutrino-matter interactions in these environments, it is extremely important to understand the flavor evolution of neutrinos, which can exhibit various collective phenomena driven by neutrino-neutrino interactions at high number densities.
An ensemble of mutually interacting neutrinos constitutes a many-body quantum system, which brings forth the possibility of the individual neutrino wavefunctions becoming ‘entangled’ with one another. Such entanglement can potentially imprint its own signatures in the flavor evolution of neutrinos (see, e.g., [1] and [2]). A commonly adopted approach, known as the ‘mean-field’ approximation, treats each neutrino as an effective one-particle system interacting with a background of other neutrinos, thereby explicitly forbidding quantum entanglement. This helps ease some of the computational complexity associated with this problem. However, the extent of the validity of the mean-field approximation remains an intriguing open question in this field.
Preliminary studies show that small-scale toy models of interacting neutrinos can exhibit deviations from the mean-field approximation, but it remains to be seen whether these deviations can persist as the particle number is increased. In general, for quantum many-body problems, it is often difficult to scale the calculations to large numbers of particles because the size of the Hilbert space grows exponentially with particle number.
In this work, we explore this problem from a different angle, namely, by analyzing the evolution of neutrino flavor and entanglement in phase space. The setup consists of two sets (beams) of neutrinos interacting with each other. We take the reduced density operator of neutrinos in one of the beams and construct its Husimi quasi-probability or “Q” representation, which consists of representing the reduced density using an over-complete basis of coherent states. Here, the “phase space” coordinates are angles θ and ϕ which describe rotations in flavor space. In the limit of infinite neutrino number, the Q representation acquires the interpretation of a classical phase-space probability distribution.
Our analysis showed that, while at early times the quasi-probability distribution remains relatively localized, at late times it develops a multimodal structure with several localized peaks (see Fig. 1). This delocalization is indicative of the entanglement being non-Gaussian in nature, which suggests that any approximate method beyond the mean-field which would limit itself to only the first and second moments of neutrino observables, may not be sufficient to describe the long-term evolution of this system.
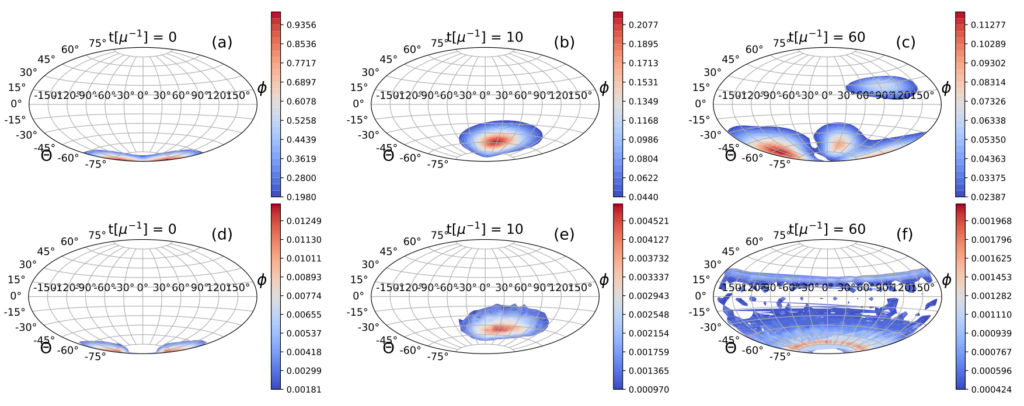
Finally, based on the phase space analysis, this paper proposes a new method for approximating the exact evolution of the interacting neutrino system. In this method, the exact quantum mechanical many-body problem is mapped on to a statistical sampling of ‘mean-field’ problems, with a Gaussian distribution of initial conditions around the exact starting point of the evolution. This approach amounts to approximating the quantum mechanical expectation values of the neutrino observances using statistical averages of their classical counterparts, which are obtained by independently evolving a large set of mean-field equations with the Gaussian-distributed initial conditions.
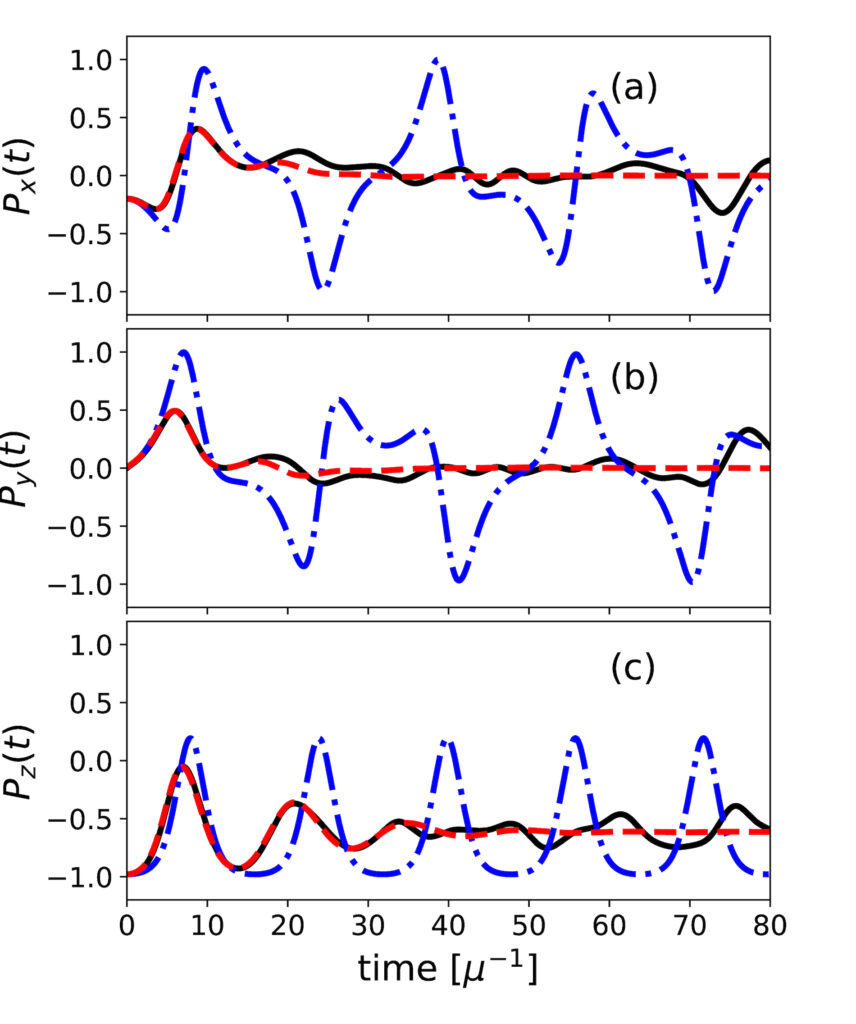
The phase-space approach with distributed initial conditions provides a simple and accurate method to describe the gross features of the neutrino flavor evolution and entanglement in the exact problem (e.g., see Fig. 2 for a comparison of neutrino flavor evolution solutions obtained using the different numerical approaches). Due to its simplicity, it is possible that this method could be more easily scalable for calculations with larger numbers of neutrinos, compared to the other approaches that go beyond the mean field. This will be explored in future work.
Read More:


