Entanglement and correlations in fast collective neutrino flavor oscillations
Prepared by Ermal Rrapaj
Collective neutrino oscillations play a crucial role in transporting lepton flavor in astrophysical settings like supernovae and neutron star binary merger remnants, which are characterized by large neutrino densities. In these settings, simulations in the mean-field approximation show that neutrino-neutrino interactions can overtake vacuum oscillations and give rise to fast collective flavor evolution on time-scales inversely proportional to the local neutrino number density. In this work, we study the full out-of-equilibrium flavor dynamics in simple multi-angle geometries displaying fast oscillations in the mean field linear stability analysis.
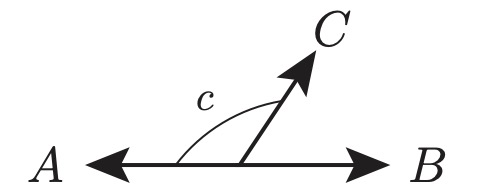
Focusing on simple initial conditions, we analyze the production of pair correlations and entanglement in the complete many-body-dynamics as a function of the number of neutrinos in the system, for up to thousands of them. Similarly to simpler geometries with only two neutrino beams, we identify three regimes: stable configurations with vanishing flavor oscillations, marginally unstable configurations with evolution occurring on long time scales, proportional to the square root of number of particles, and unstable configurations showing flavor evolution on short time scales proportional to the logarithm of the number of particles.
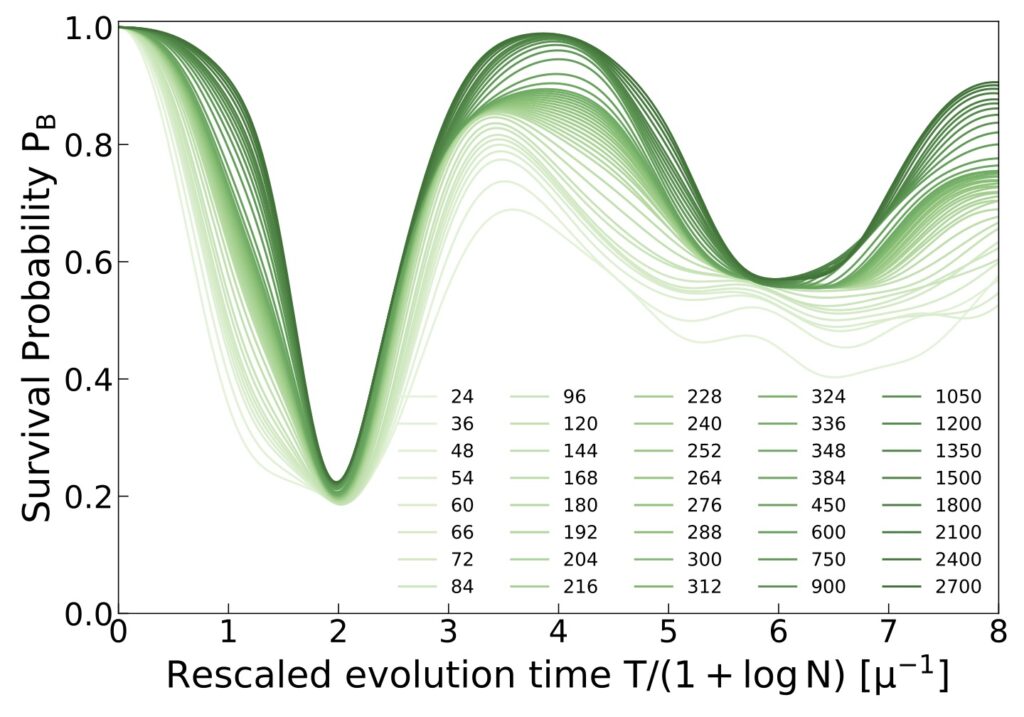
The plot uses a rescaled time variable (darker colors indicate larger values of N) to highlight the system size dependence.
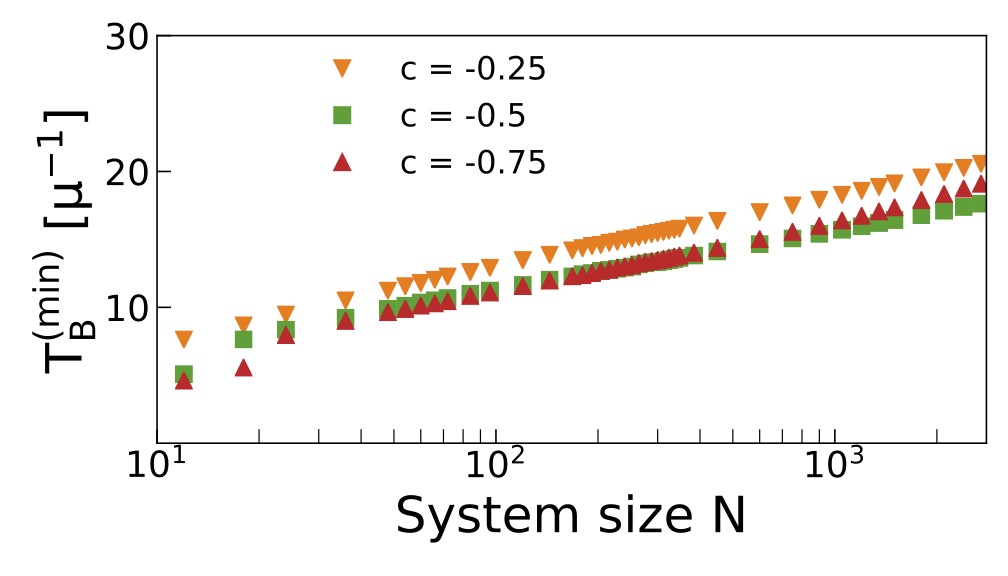
The straight lines for -1<c<0 emphasize the logarithmic dependence on system size for unstable configurations.
We present evidence that these fast collective modes are generated by the same dynamical phase transition which leads to the slow bipolar oscillations, establishing a connection between these two phenomena and explaining the difference in their time scales. We conclude by discussing a semi-classical approximation which reproduces the entanglement entropy at short to medium time scales and can be potentially useful in situations with more complicated geometries where classical simulation methods start to become inefficient.
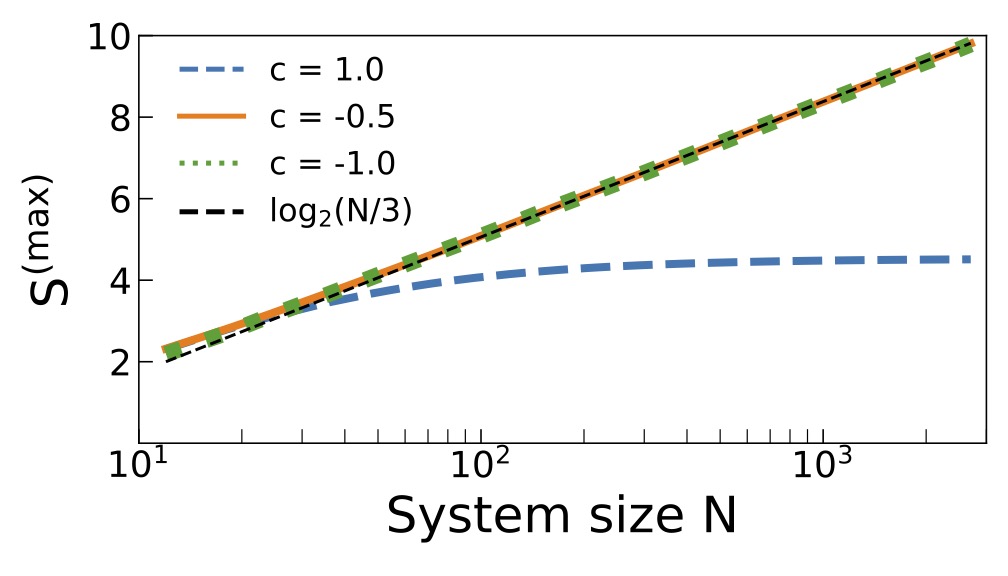
For comparison, we have also included the dashed black line to show the functional form of the system size dependence.
Read More: