Where they split, they entangle: A (collective) neutrino story
Neutrinos do not experience strong or electromagnetic interactions, and are therefore by far the most feebly interacting among all the known particles in the universe. Nevertheless, there are situations where the sheer strength in numbers can make up for the weakness of the interaction — notably, in extreme astrophysical environments such as core-collapse supernovae, mergers of neutron stars, and in the early universe. Their unique combination of physical characteristics (electrically neutral and extremely lightweight) makes neutrinos extremely efficient at carrying energy and lepton number, giving them a crucial role to play in the dynamics and in the synthesis of elements in these environments.
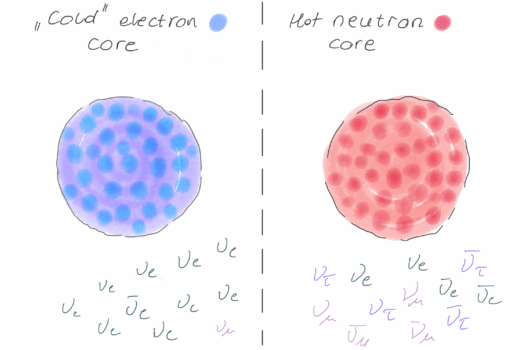
Neutrinos come in multiple flavors (electron, muon, and tau), and are known to be able to oscillate between these flavors. In an environment where the high densities of neutrinos permit substantial neutrino-neutrino interactions, each neutrino can influence the oscillation patterns of the other neutrinos that it interacts with. This gives rise to an extremely complex, interacting system of coupled oscillators, leading to various kinds of collective features being exhibited in the neutrino flavor oscillation patterns. One such collective feature is known as the “spectral split” — which are sharp transitions in the flavor conversion probabilities at certain points in the neutrino energy spectra.
An intriguing possibility brought about by the interactions among neutrinos is that of quantum entanglement. In an entangled system of particles, the wavefunction representing the quantum state of the system cannot be factorized into wavefunctions of individual particles. Theoretical studies of entangled systems are usually limited to only small numbers of particles (of order 10), because the computational cost of simulating these systems (both in terms of time and memory) grows exponentially with increasing particle number. Naturally, simulating the flavor evolution of 1058 coupled neutrinos in a core-collapse supernova environment is an impossible undertaking, and therefore various approximations are required. One such approximation, known as the “mean-field approximation”, explicitly forbids the possibility of quantum entanglement, thereby forcing the wavefunction of the many-body neutrino system to always remain factorizable into single-particle wavefunctions. This greatly reduces the computational complexity of the problem to linear rather than exponential, making it possible to simulate the flavor evolution of up to a million interacting neutrinos at once.
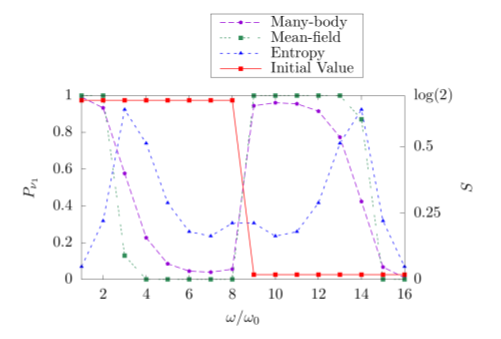
Our work is aimed at testing the fidelity of the mean-field approximation, albeit using an extremely simplified model with up to 16 neutrinos. In our calculations, we simulate and compare the flavor evolution of interacting neutrino systems both with and without the inclusion of quantum entanglement. If the amount of entanglement, as quantified by the “entanglement entropy”, were found to be substantial in the simulation where it is permitted to grow, then that would be an indication that the mean-field simulation could be missing out on potentially important details. In particular, entangled neutrino systems could exhibit flavor oscillation features that are different from those seen in the mean-field calculations.
We found in our simplified model that the growth of entanglement is most significant amongst the neutrinos that are closest to the spectral splits in the energy spectrum. A consequence of this entanglement is that the splits appear much more smeared compared to those in the mean-field calculations, as shown in the figure below. This observation suggests a path forward for exploring entanglement effects and testing the mean-field efficacy in systems with larger numbers of neutrinos. By allowing the entanglement to grow only near the spectral splits while restricting it elsewhere across the spectrum, the computational complexity may scale much more favorably compared to a system which permits unrestricted entanglement growth throughout the ensemble. Such hybrid approaches shall be the subject of future investigations.
This introduction was prepared by N3AS fellow Amol Patwardhan
Read More: