Oscillations of Highly Magnetized Non-Rotating Neutron Stars

Prepared by Patrick Chi-Kit Cheong

Neutron stars are probably the most compact and extreme magnetised astrophysical objects in the universe. These stars are the composite of the most extreme physics within only a few kilometres in diameter. For instance, of a comparable size to a small city, these compact objects could be as massive as stars due to their extremely high densities. The resulting gravitational field is so strong that it induces significant distortion in spacetime.

In addition to their ultra-strong compactness and enormous gravity, neutron stars harbour unbelievably intense, long-lived, large-scale magnetic fields. The magnetic field strength of typical neutron stars, also known as pulsars, could reach at least $\sim 10^{8-13}$ Gauss (G), with orders of magnitude higher than in any other object. The strength of neutron star magnetic field could be even more extreme and exotic, which goes beyond $10^{15}$ G, up to 1000 times stronger than typical neutron stars.

The unbelievably intense magnetic fields they carry are known to be responsible for many astrophysical phenomena. Therefore, understanding the origin and properties of these extreme magnetic fields are the key to solve many puzzling problems on highly energetic astrophysical phenomena. However, although roughly 3000 neutron stars have been discovered since 1968, only little has been known about their magnetic fields. The way neutron stars oscillate is very likely to be imprinted in their gravitational waves and electromagnetic emissions, which can be detected via different detectors. These oscillations, not only heavily related to the stars internal structures and composition, but also significantly related the topologies and strength of the ultra-strong magnetic fields carried by them (see also this article). Therefore, understanding the properties of neutron star oscillations is very important.

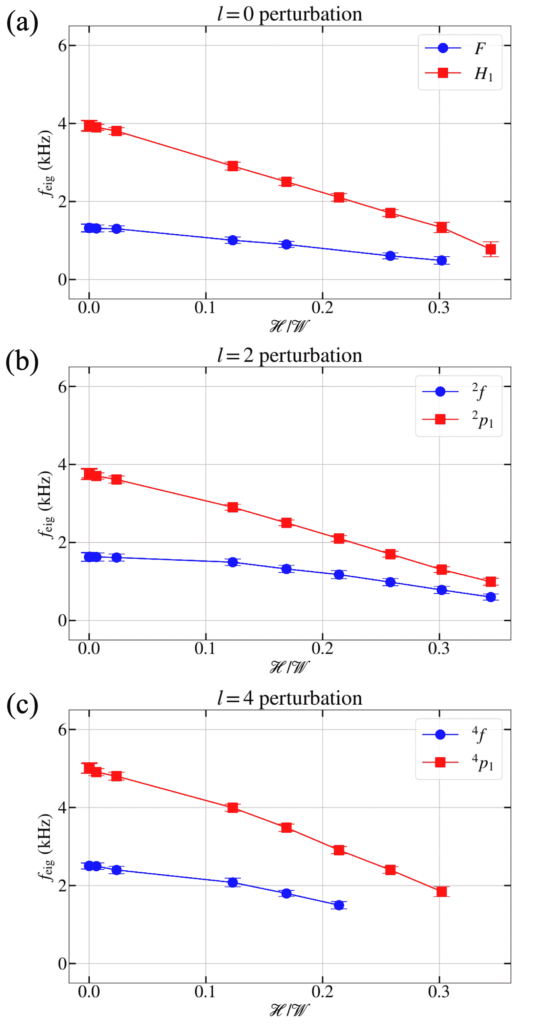
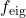Three graphs, a, b, and c. — Eigenfrequencies $f_{\textrm{eig}}$ of the excited oscillation modes against the magnetic to binding energy ratio 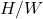$\mathscr{H}/\mathscr{W}$ of the NS model, if 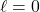$\ell=0$ (*Upper panel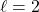*), $\ell=2$ (*Middle panel*), and 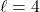$\ell=4$ (*Lower panel*) perturbations are applied respectively.
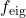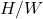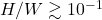As shown in the figure, $f_{\textrm{eig}}$ noticeably decreases with $\mathscr{H}/\mathscr{W}$ for $\mathscr{H}/\mathscr{W} \gtrsim 10^{-1}$ in general.
We can see that stellar oscillations are significantly suppressed by stronger magnetization for NSs with $\mathscr{H}/\mathscr{W} \gtrsim 10^{-1}$ .

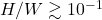In this work, we have studied how the ultra-high purely toroidal magnetic fields affect the structure of neutron stars, and the corresponding oscillations. We found that the oscillations frequencies of the stars decrease as the magnetic field increase (as shown in the fig.~1). The suppression of frequencies is significant when the magnetic energy consist more than ~10% of the binding energy of the systems. This suppression can be understood by the fact that the oscillation frequency is positivity correlated to the compactness of the stars. We have shown that given the same mass of the neutron stars, the compactness decrease as the magnetic field increase because of the contribution of the magnetic pressure. Therefore, as a direct consequence of lower compactness, the oscillation frequencies of the neutron stars with stronger magnetic fields is lower (as shown in the fig.~2).

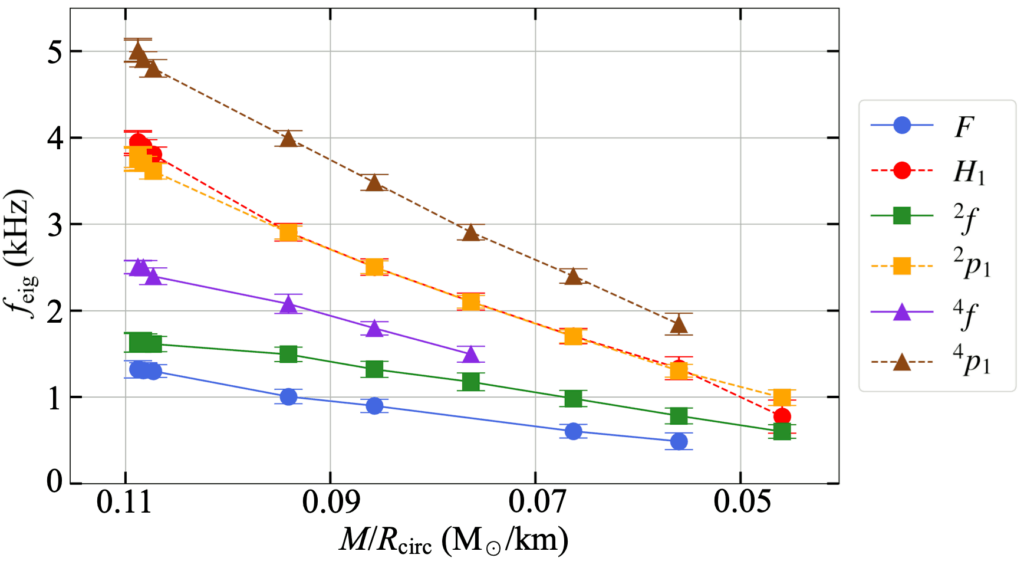
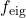Eigenfrequencies $f_{\rm eig}$ of the excited oscillation modes are plotted against compactness 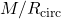$M/R_{\rm circ}$ of the NS model, where 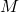$M$ is the gravitational mass and 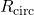$R_{\rm circ}$ is the circumferential radius. All data points show that 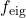$f_{\rm eig}$ decreases together with 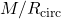$M/R_{\rm circ}$ in an almost linear way. Hence, this demonstrates a quasilinear relation between eigenfrequencies of oscillation modes and stellar compactness for magnetised NSs.

This work presents the first step to understanding how magnetic fields affect the oscillations of neutron stars. In the future, we will also study how the topologies/strength of the magnetic fields affect the oscillations, with more realistic equations of states, and with full 3-dimensional simulations.