What can we learn from 1018 Muons? Probing Flavor Violation in the Laboratory

Prepared by Evan Rule

Flavor violation among the neutrinos, discovered in solar and atmospheric neutrino experiments, suggests—and indeed requires—flavor violation among the neutrino’s charged partners, the electron, muon, and tau. When a muon decays into an electron, the process is always seen to conserve lepton flavor, the most common decay being $\mu^-\rightarrow e^- + \bar{\nu}_e+\nu_\mu$ . The charged lepton flavor-violating (CLFV) decay $\mu^-\rightarrow e^-+\gamma$ has never been observed, though there are many plausible extensions of the standard model, including supersymmetry, leptoquarks, heavy neutrinos, or a more complicated Higgs sector, that predict a small but non-zero rate for this process.

One of the most tightly constrained CLFV processes is $\mu \to e$ conversion, where the muon is captured onto an atomic nucleus. The bound muon has a precisely known energy, and if it were to convert to an electron and zero neutrinos (without exciting the nucleus), then the resulting electron would have exactly the energy of the bound muon, called the endpoint energy. Electrons that come from standard model decays with two final state neutrinos must have energies below the endpoint energy. Thus, any observation of an electron at the endpoint energy is evidence of CLFV and a definite sign of physics beyond the standard model.

The fact that this process has never been observed—despite significant experimental efforts—places constraints on new physics at high energies. For example, the SINDRUM II experiment tells us that $\mu \to e$ conversion must be more rare than a one-in-1 trillion event, which, depending on the underlying mechanism, rules out sources of CLFV up to 900 TeV.

A new generation of experiments, Mu2e at Fermilab and COMET at Japan’s J-PARC, are aiming to improve the experimental sensitivity on $\mu \to e$ conversion by a factor of 10,000 by the end of the decade. This incredible advance in sensitivity provides a huge window for discovery of new physics, probing scales as high as 10,000 TeV. Mu2e and COMET will each capture and observe muons over their respective lifetimes, looking for just a single $\mu \to e$ conversion event. Both experiments have chosen $^{27}$ Al as the nuclear target, though additional constraints can be obtained by varying the target.

One major challenge to interpreting the results of $\mu \to e$ conversion experiments is that the observations are made at nuclear energies $\approx100$ MeV, whereas the BSM physics that is responsible for CLFV is typically associated with some very high energy scale $\gtrsim 10$ TeV. BSM theories that look quite different at 1,000 TeV may yield identical observations in $\mu \to e$ conversion experiments. In our work, we developed a nuclear effective theory of $\mu \to e$ conversion in order to delineate what can and cannot be learned about the form of new physics through these measurements.

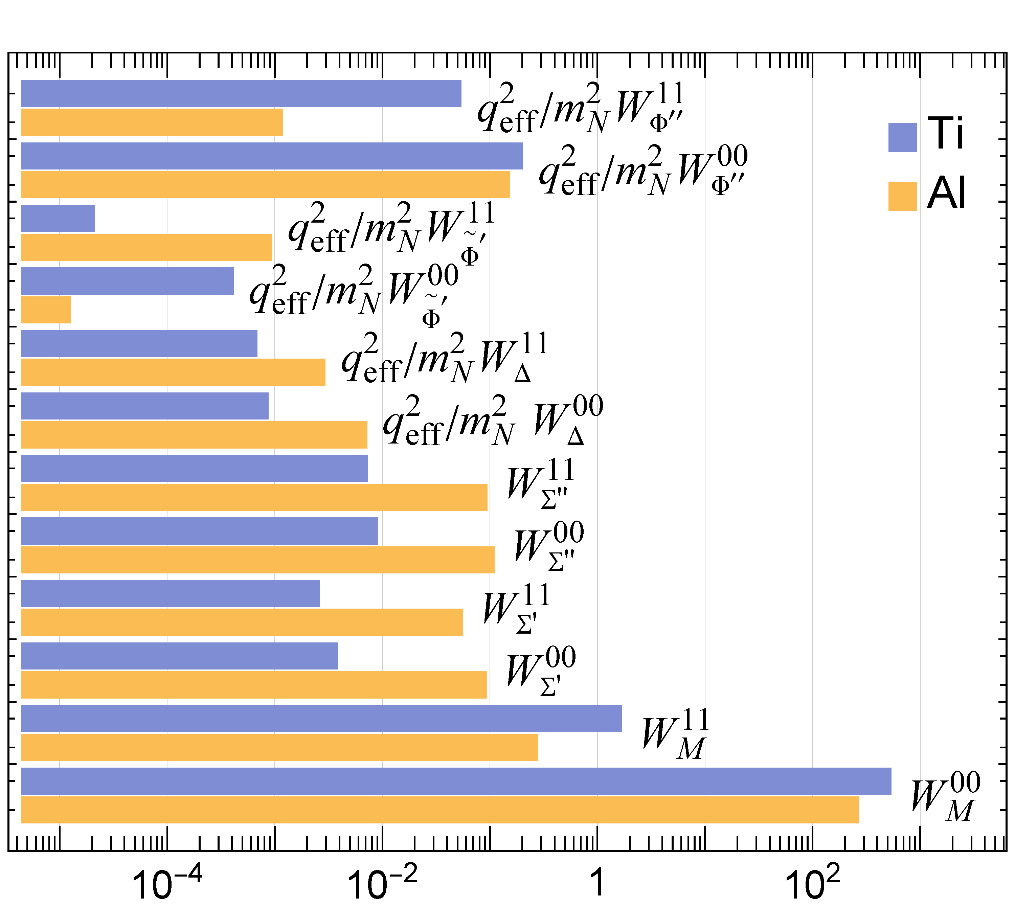
Figure 1: Comparison of nuclear response functions that arise in elastic $\mu \to e$ conversion in two targets, Al and Ti. Superscript “00” denotes isoscalar coupling (equal proton/neutron couplings) whereas “11” denotes isovector (equal and opposite proton/neutron couplings). $q_\mathrm{eff}$ is the magnitude of the effective three-momentum transfer. The responses may be classified by their dependence on nuclear spin and velocity as

Spin- and velocity-independent: $M$
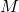
Spin-dependent and velocity-independent: $\Sigma',\Sigma''$
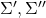
Spin-independent and velocity-dependent: $\Delta$
Spin- and velocity-dependent: $\tilde{\Phi}',\Phi''$

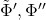
Among other differences, the contrast between Al and Ti is ideal for distinguishing between spin-dependent and spin-independent sources of CLFV.

We find that there are only 6 independent nuclear responses that are probed when the conversion process takes place in a nuclear system. This number is doubled to 12 when we account for the fact that the new physics may couple differently to protons than to neutrons. The relative strengths of these 12 responses depend sensitively on the choice of nuclear target, as shown in Fig. 1.

In determining the expected rate for $\mu \to e$ conversion in a given target, each nuclear response function $W$ is multiplied by some unknown factor, which we call $R$ , that encodes all of the CLFV physics. These $R$ coefficients are the parameters that one can measure directly in experiments like Mu2e and COMET. If two BSM theories yield different values for the $R$ coefficients, then they can be distinguished by $\mu \to e$ conversion experiments in different targets, otherwise they cannot.

Header photo: A segment of the Mu2e transport solenoid that will use superconducting magnets in order to focus roughly 10 billion muons per second onto the aluminum stopping target. Credit: Vito Lombardo, Fermilab

Read More: